331 验证二叉树的前序序列化(Medium)
序列化二叉树的一种方法是使用 前序遍历 。当我们遇到一个非空节点时,我们可以记录下这个节点的值。如果它是一个空节点,我们可以使用一个标记值记录,例如 #。
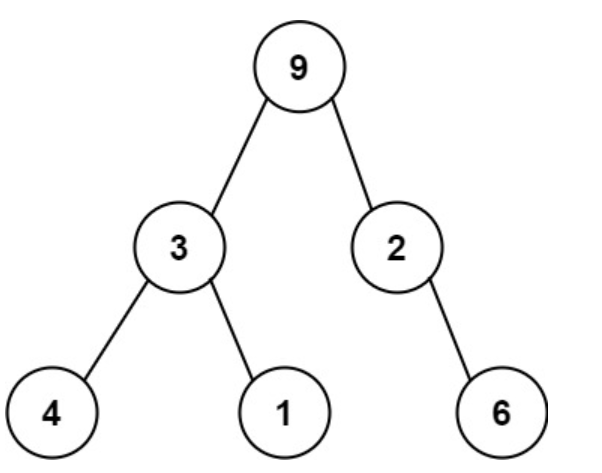
例如,上面的二叉树可以被序列化为字符串 “9,3,4,#,#,1,#,#,2,#,6,#,#”,其中 # 代表一个空节点。
给定一串以逗号分隔的序列,验证它是否是正确的二叉树的前序序列化。编写一个在不重构树的条件下的可行算法。
保证 每个以逗号分隔的字符或为一个整数或为一个表示 null 指针的 ‘#’ 。
你可以认为输入格式总是有效的
例如它永远不会包含两个连续的逗号,比如 “1,,3” 。
注意:不允许重建树。
栈
由于是先序遍历,我们考虑栈。栈的存放一个数组,第一位表示在split中的下标,第二位表示左边是否有节点,第三位表示右边是否有节点
遍历这个数组,然后如果栈非空,当前元素就是栈顶元素的左孩子或者右孩子,更新栈顶数组,每次遍历都要判断栈顶元素是否左右都有,如果有就出栈。
遍历完看栈是否为空,为空说明是二叉树
这里有两个细节,
- 首先是可能出现多棵树的情况,也就是说以上算法对于两个完整的树拼在一起的字符串结果还是为true,需要一个计数器,如果在循环过程中栈就已经空了,就返回false
- 还有就是这里用了trycatch,如果出现异常情况比如栈顶为空了,那肯定是出问题了,直接返回false,也算是一种偷懒吧。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| public boolean isValidSerialization(String preorder) {
try {
int count = 0;
String[] split = preorder.split(",");
if (split.length == 1 && Objects.equals(split[0], "#")){
return true;
}
Stack<int[]> stack = new Stack<>();
for (int i = 0; i < split.length; i++) {
if (!Objects.equals(split[i], "#")){
if (!stack.isEmpty()){
if (stack.peek()[1] ==0 && stack.peek()[2] == 0){
stack.peek()[1] = 1;
}
else if (stack.peek()[1] == 1 && stack.peek()[2] == 0){
stack.peek()[2] = 1;
}
}
stack.add(new int[]{i,0,0});
}
else {
if (stack.peek()[1] == 0 && stack.peek()[2] ==0){
stack.peek()[1] = 1;
}
else if (stack.peek()[1] == 1 && stack.peek()[2] == 0){
stack.peek()[2] = 1;
}
}
while (!stack.isEmpty() && stack.peek()[1] == 1 && stack.peek()[2] == 1){
stack.pop();
}
if (stack.isEmpty() && i != split.length-1){
count++;
}
}
if (count!=0){
return false;
}
return stack.isEmpty();
}
catch (Exception e){
return false;
}
}
|
时间复杂度:O(n),其中 n 为字符串的长度。我们每个字符只遍历一次,同时每个字符对应的操作都是常数时间的。
空间复杂度:O(n)。此为栈所需要使用的空间。
