因为第三题long被卡了三发wa，所以即使做出了第三题也没上次排名高

第一题：哈沙德数

如果一个整数能够被其各个数位上的数字之和整除，则称之为 哈沙德数（Harshad number）。给你一个整数 x 。如果 x 是 哈沙德数 ，则返回 x 各个数位上的数字之和，否则，返回 -1 。

字符串拆分成数组，然后累计和，最后做个判断

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public int sumOfTheDigitsOfHarshadNumber(int x) {
        String num = ""+x;
        String[] split = num.split("");
        int ans = 0;
        //System.out.println(Arrays.toString(split));
        for (int i = 0; i < split.length; i++) {
            ans+=Integer.parseInt(split[i]);
        }
        if (x % ans ==0){
            return ans;
        }
        else {
            return -1;
        }
    }
}

第二题：换水问题

给你两个整数 numBottles 和 numExchange 。

numBottles 代表你最初拥有的满水瓶数量。在一次操作中，你可以执行以下操作之一：

  • 喝掉任意数量的满水瓶，使它们变成空水瓶。
  • 用 numExchange 个空水瓶交换一个满水瓶。然后，将 numExchange 的值增加 1 。
    注意，你不能使用相同的 numExchange 值交换多批空水瓶。例如，如果 numBottles == 3 并且 numExchange == 1 ，则不能用 3 个空水瓶交换成 3 个满水瓶。

返回你 最多 可以喝到多少瓶水。

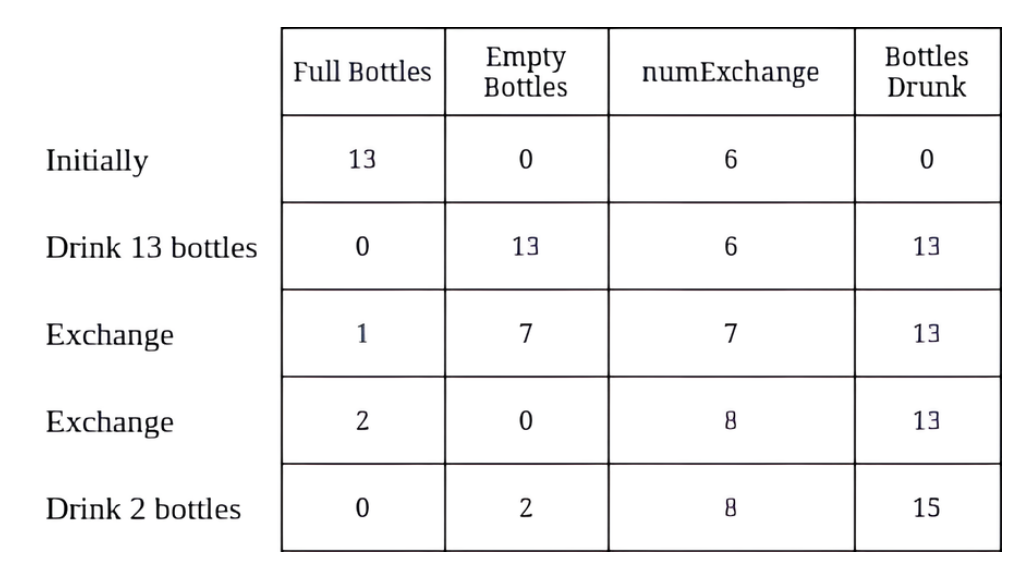
小学奥数貌似碰到过这样的问题，就是没兑换一次，兑换的要求就多一瓶，直接暴力模拟就行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int maxBottlesDrunk(int numBottles, int numExchange) {
        int empty = numBottles;
        int ans = numBottles;
        //直到换不了了
        while (empty >= numExchange){
            //兑换新的之后剩下的
            empty -=numExchange;
            numExchange++;
            //兑换多的
            empty +=1;
            ans++;
        }
        return ans;
    }
}

第三题：交替子数组计数

给你一个二进制数组nums 。

如果一个子数组中 不存在 两个 相邻 元素的值 相同 的情况，我们称这样的子数组为 交替子数组 。

返回数组 nums 中交替子数组的数量。

示例 1：

输入： nums = [0,1,1,1]

输出： 5

解释： 以下子数组是交替子数组：[0] 、[1] 、[1] 、[1] 以及 [0,1] 。

这里有个用例真的好恶心，wa三次都是这一个用例没过，需要全开long或者long long才能过

记忆化搜索超出内存限制

最早的思路是用一个二维数组存dp[i][j]是否是一个交替子数组，为1表示i到j是一个交替子数组，判断条件$$ dp[i][j-1] == 1 && nums[j] != nums[j-1] $$

其实完全不用这么大的空间，二维数组超空间也是应该的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
    public long countAlternatingSubarrays(int[] nums) {
        //记忆化搜索
        int[][] dp = new int[nums.length][nums.length];
        for (int i = 0; i < nums.length; i++) {
            for (int j = i; j < nums.length; j++) {
                //对角线肯定是交替子数组
                if (i==j){
                    dp[i][j] = 1;
                }
                else {
                    //只有前面是一个交替子数组并且不等于最后的那个元素
                    if (dp[i][j-1] == 1 && nums[j] != nums[j-1]){
                        dp[i][j] = 1;
                    }
                    else {
                        dp[i][j] = 0;
                    }
                }
            }
        }
        //最后再遍历一次数组，每一个1就是一个交替子数组
        long ans = 0;
        for (int i = 0; i < nums.length; i++) {
            for (int j = i; j < nums.length; j++) {
                if (dp[i][j] == 1){
                    ans+=1;
                }
            }
        }
        return ans;

    }
}

双指针(AC)

思路是，如果一个数组是交替数组，那么子数组肯定也是，利用双指针找到尽量最长的交替子数组存起来，最后遍历这些最长的交替子数组。由于他们的子数组肯定也是交替的，那就是等差数列求和就可以算出。最后累加得到答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public long countAlternatingSubarrays(int[] nums) {
        //恶心的long
        List<long[]> list = new ArrayList<>();
        long head = 0;
        long rear = 0;
        //双指针找到长的数组，存起来他们的下标
        for (int i = 1; i < nums.length; i++) {
            if (nums[i] == nums[i-1]){
                list.add(new long[]{head,rear});
                head = i;
            }
            rear++;
        }
        //最后一个没加上就退出循环了，需要最后加上
        list.add(new long[]{head,rear});
        long ans = 0;
        for (int i = 0; i < list.size(); i++) {
            long length = list.get(i)[1]-list.get(i)[0]+1;
            //子数组的数量
            ans += length *(length+1)/2;
        }
        return ans;
    }
}

时间复杂度:o(n)
空间复杂度：o(n)