经过一天的冲业绩终于上了200题,说实话有点追求数量不追求质量了。但是我确实也感觉记性没以前那么好了,菜就多练。
2908 元素和最小的山形三元组(Eazy)
给你一个下标从 0 开始的整数数组 nums 。
如果下标三元组$ (i, j, k) $满足下述全部条件,则认为它是一个 山形三元组 :
- $i < j < k$
- $nums[i] < nums[j]$ 且 $nums[k] < nums[j]$
请你找出 nums 中 元素和最小 的山形三元组,并返回其 元素和 。如果不存在满足条件的三元组,返回 -1 。
示例 1:
输入:$nums = [8,6,1,5,3]$
输出:9
解释:三元组 (2, 3, 4) 是一个元素和等于 9 的山形三元组,因为:
- 2 < 3 < 4
- $nums[2] < nums[3]$ 且 $nums[4] < nums[3]$
这个三元组的元素和等于 $nums[2] + nums[3] + nums[4] = 9$ 。可以证明不存在元素和小于 9 的山形三元组。
暴力枚举(居然没超时)
没什么好说的直接遍历所有三元组,判断是否是山形
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
public int minimumSum(int[] nums) {
int min = Integer.MAX_VALUE;
for (int i = 0; i < nums.length - 2; i++) {
for (int j = i+1; j < nums.length-1; j++) {
for (int k = j+1; k < nums.length; k++) {
if (nums[i] < nums[j] && nums[j] >nums[k]){
min = Math.min(min,nums[i]+nums[j]+nums[k]);
}
}
}
}
if (min == Integer.MAX_VALUE){
min = -1;
}
return min;
}
}
|
时间复杂度:o(n^3),这么高的复杂度没超时就算了,居然还77%?有点搞笑了
空间复杂度:o(1),只用了一个min来保存最大值
有效的括号(Easy)
今天的主菜是各种栈,先从最简单的说起
给定一个只包括 ‘(‘,’)’,’{‘,’}’,’[‘,’]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 每个右括号都有一个对应的相同类型的左括号。
示例 1:
输入:s = “()”
输出:true
示例 2:
输入:s = “()[]{}”
输出:true
示例 3:
输入:s = “(]”
输出:false
简单栈
最基础的括号匹配问题,所有左边括号进栈,如果能和右边括号匹配就出栈,到最后如果还有括号没有匹配上,就返回false,如果为空就是true
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| class Solution {
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
boolean flag = true;
for (int i = 0; i < s.length(); i++) {
char temp = s.charAt(i);
if (temp == '}'){
if (!stack.isEmpty()&&stack.peek() == '{'){
stack.pop();
}
else {
flag = false;
}
}
else if (temp == ')'){
if (!stack.isEmpty()&&stack.peek() == '('){
stack.pop();
}
else {
flag = false;
}
}
else if (temp == ']'){
if (!stack.isEmpty()&&stack.peek() == '['){
stack.pop();
}
else {
flag = false;
}
}
else stack.push(temp);
}
return flag & stack.isEmpty();
}
}
|
时间复杂度:o(n)
空间复杂度:o(n),因为维护了一个栈
394 字符串解码(Medium)
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: $k[encoded_string]$,表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
示例 1:
输入:s = “3[a]2[bc]”
输出:”aaabcbc”
示例 2:
输入:s = “3[a2[c]]”
输出:”accaccacc”
简单栈
先进后出,又是用栈的经典问题,维护两个栈,一个放数字,一个放符号,这里考虑到数字也会又多位数字,所以在字符串中需要特意考虑多位数字。
另一个栈用于放字符串,这里刚开始考虑用Char的栈,但是这样就会频繁出栈入栈,所以还不如就用字符串。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
| class Solution {
public String decodeString(String s) {
Stack<String> stack = new Stack<>();
Stack<Integer> numstack = new Stack<>();
for (int i = 0; i < s.length();) {
if (judgeNumOrChar(s.charAt(i))){
StringBuilder num = new StringBuilder();
while (judgeNumOrChar(s.charAt(i))){
num.append(s.charAt(i));
i++;
}
numstack.push(Integer.parseInt(num.toString()));
}
else {
if (s.charAt(i) != ']'){
stack.push(""+s.charAt(i));
}
else {
StringBuilder temp = new StringBuilder();
int count = numstack.pop();
while (!Objects.equals(stack.peek(), "[")){
temp.insert(0, stack.pop());
}
stack.pop();
for (int j = 0; j < count; j++) {
stack.push(temp.toString());
}
}
i++;
}
}
StringBuilder ans = new StringBuilder();
while (!stack.isEmpty()){
ans.insert(0, stack.pop());
}
return ans.toString();
}
public boolean judgeNumOrChar(Character character){
return (character < 'a' || character > 'z') && character != '[' && character != ']';
}
}
|
时间复杂度o(n)
空间复杂度,就是解码出的字符串的长度,这个没办法跟n有关
739 每日温度(Medium)
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
单调栈
维护一个存储下标的单调递减栈,当要进入的元素比栈顶元素大的时候,弹出栈顶,那么栈顶对应的今日最高温度就是当前这个,数组中放进两者的日期差值,以此循环。直到进入元素比栈顶小
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution {
public int[] dailyTemperatures(int[] temperatures) {
Stack<int[]> monoStack = new Stack<>();
int[] ans = new int[temperatures.length];
for (int i = 0; i < temperatures.length; i++) {
while (!monoStack.isEmpty() && monoStack.peek()[0] < temperatures[i]){
int[] latest = monoStack.pop();
ans[latest[1]] = i-latest[1];
}
monoStack.push(new int[]{temperatures[i],i});
}
while (!monoStack.isEmpty()){
int[] latest = monoStack.pop();
ans[latest[1]] = 0;
}
return ans;
}
}
|
时间复杂度o(n)
空间复杂度o(n)
接下来是两个单调栈难题
84 柱状图中最大的矩形(Hard)
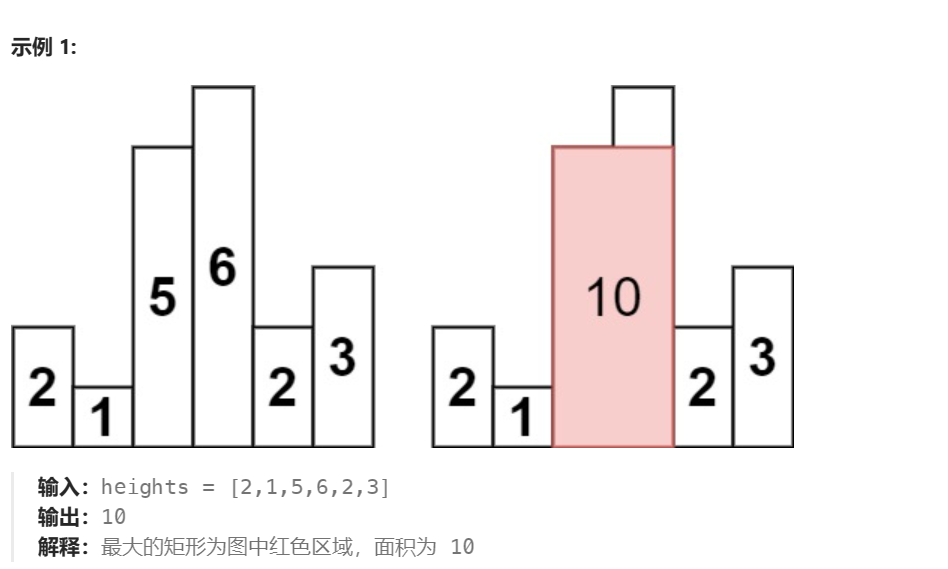
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1 。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
单调栈
假设当前元素nums[i],我只要找到在他左边第一个比当前元素小,和右边第一个比当前元素小的,那么他们围成的矩形的高度就是nums[i],长度就是右边-左边-1(因为实际上不能到比它小的位置),
这样问题就简化了,有了左边右边这些元素,只需要遍历一次,计算(右边-左边-1)*当前元素,找到最大值就是答案。
那么怎么样找到这些第一个比它小的元素呢,用单调栈
对于左边来说,维护一个单调递增的栈,那么每一个比栈顶进去大的元素,最左边第一个比它小的元素肯定是栈顶的。如果进入元素比栈顶小,那就一直出栈,直到进入元素比栈顶大,这个时候出栈的元素肯定都是大于当前元素的,
也就是不是最左边比它小的元素,此时栈顶的才比它小,这就算出了最左边比它小的元素位置,但是如果此时栈空了,说明左边的全比自己大,那就返回-1.
右边的同理,只不过栈空对应的是nums.length
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| class Solution {
public int largestRectangleArea(int[] nums) {
Stack<Integer> stack = new Stack<>();
int[] left = new int[nums.length];
int[] right = new int[nums.length];
for (int i = 0; i < nums.length; i++) {
while (!stack.isEmpty() && nums[stack.peek()] >= nums[i]){
stack.pop();
}
if (stack.isEmpty()){
left[i] = -1;
}
else {
left[i] = stack.peek();
}
stack.push(i);
}
stack = new Stack<>();
for (int i = nums.length-1; i >= 0; i--) {
while (!stack.isEmpty() && nums[stack.peek()] >= nums[i]){
stack.pop();
}
if (stack.isEmpty()){
right[i] = nums.length;
}
else {
right[i] = stack.peek();
}
stack.push(i);
}
int max = Integer.MIN_VALUE;
for (int i = 0; i < nums.length; i++) {
max = Math.max(max,(right[i]-left[i]-1)*nums[i]);
}
return max;
}
}
|
很重要这个题,这种思想已经不是第一次见到了,分别按照左边右边两个数组,遍历三次
时间复杂度:o(n)
空间复杂度:o(n)
接雨水(Hard)
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。

动态规划
其实也用了上一题的思想
对于下标 i,下雨后水能到达的最大高度等于下标 i 两边的最大高度的最小值,下标 i 处能接的雨水量等于下标 i 处的水能到达的最大高度减去 height[i]。
朴素的做法是对于数组 height 中的每个元素,分别向左和向右扫描并记录左边和右边的最大高度,然后计算每个下标位置能接的雨水量。假设数组 height 的长度为 n,该做法需要对每个下标位置使用 O(n) 的时间向两边扫描并得到最大高度,因此总时间复杂度是 O(n^2)
上述做法的时间复杂度较高是因为需要对每个下标位置都向两边扫描。如果已经知道每个位置两边的最大高度,则可以在 O(n)的时间内得到能接的雨水总量。使用动态规划的方法,可以在 O(n) 的时间内预处理得到每个位置两边的最大高度。
创建两个长度为 n 的数组 leftMax 和 rightMax。对于 0≤i<n0 ,leftMax[i] 表示下标 i 及其左边的位置中,height 的最大高度,rightMax[i] 表示下标 i 及其右边的位置中,height 的最大高度。
显然,$leftMax[0]=height[0]$,$rightMax[n−1]=height[n−1]$。两个数组的其余元素的计算如下:
- 当 $1≤i≤n−1$ 时,$leftMax[i]=max(leftMax[i−1],height[i])$;
- 当 $0≤i≤n−2$ 时,$rightMax[i]=max(rightMax[i+1],height[i])$。
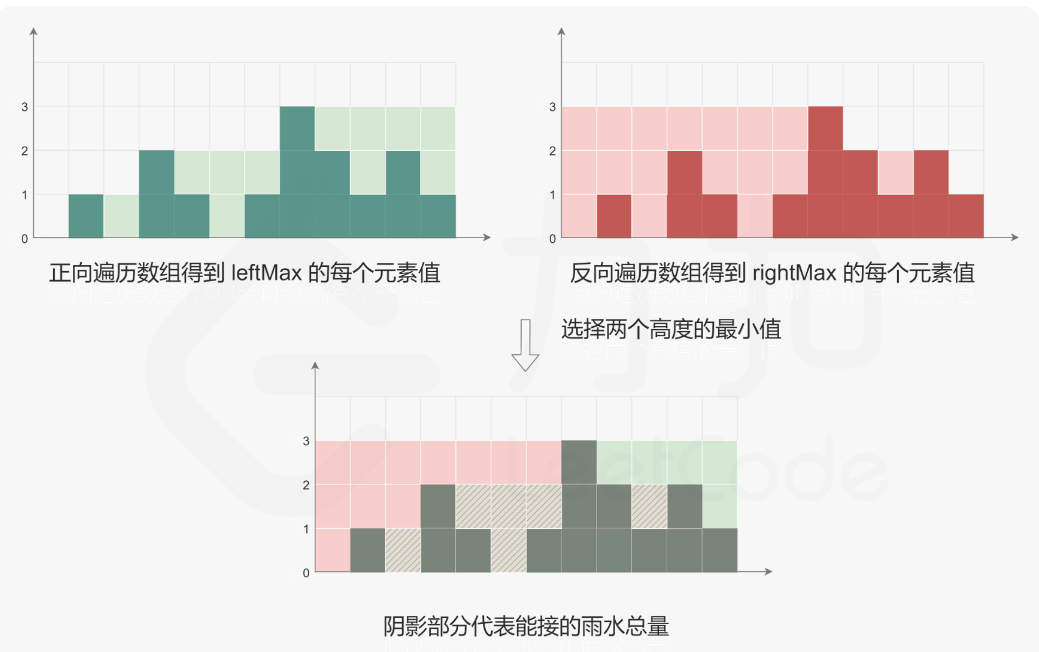
因此可以正向遍历数组 height 得到数组 leftMax 的每个元素值,反向遍历数组 height 得到数组 rightMax 的每个元素值。
在得到数组 leftMax 和 rightMax 的每个元素值之后,对于 0≤i<n,下标 i 处能接的雨水量等于 $min(leftMax[i],rightMax[i])−height[i]$。遍历每个下标位置即可得到能接的雨水总量。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public int trap(int[] height) {
int[] left = new int[height.length];
left[0] = height[0];
int[] right = new int[height.length];
right[height.length-1] = height[height.length-1];
for (int i = 1; i < height.length; i++) {
left[i] = Math.max(left[i-1],height[i]);
}
for (int i = height.length-2; i >=0 ; i--) {
right[i] = Math.max(right[i+1],height[i]);
}
int ans = 0;
for (int i = 0; i < height.length; i++) {
ans += Math.min(left[i],right[i])-height[i];
}
return ans;
}
}
|
单调栈
这个挺难理解的
除了计算并存储每个位置两边的最大高度以外,也可以用单调栈计算能接的雨水总量。
维护一个单调栈,单调栈存储的是下标,满足从栈底到栈顶的下标对应的数组 height 中的元素递减。
从左到右遍历数组,遍历到下标 i 时,如果栈内至少有两个元素,记栈顶元素为 top,top 的下面一个元素是 left,则一定有 $height[left]≥height[top]$。如果 $height[i]>height[top]$,则得到一个可以接雨水的区域,该区域的宽度是 $i−left−1$,高度是 $min(height[left],height[i])−height[top]$,根据宽度和高度即可计算得到该区域能接的雨水量。
为了得到 left,需要将 top 出栈。在对 top 计算能接的雨水量之后,left 变成新的 top,重复上述操作,直到栈变为空,或者栈顶下标对应的 height 中的元素大于或等于 height[i]。
在对下标 i 处计算能接的雨水量之后,将 i 入栈,继续遍历后面的下标,计算能接的雨水量。遍历结束之后即可得到能接的雨水总量。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public int trap(int[] height) {
Stack<Integer> stack = new Stack<>();
int ans = 0;
for (int i = 0; i < height.length; i++) {
while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
int top = stack.pop();
if (stack.isEmpty()) {
break;
}
int left = stack.peek();
int currWidth = i - left - 1;
int currHeight = Math.min(height[left], height[i]) - height[top];
ans += currWidth * currHeight;
}
stack.push(i);
}
return ans;
}
}
|



