今天斗胆试了一下蓝桥杯的题，实在是感觉太难了，不暴力根本不会做，以后有机会再写题解吧。

我觉得这种程序设计竞赛还是得好好研究算法才行，我这种野路子还有很长一段路要走

1997 访问完所有房间的第一天（Medium）

你需要访问 n 个房间，房间从 0 到 n - 1 编号。同时，每一天都有一个日期编号，从 0 开始，依天数递增。你每天都会访问一个房间。

最开始的第 0 天，你访问 0 号房间。给你一个长度为 n 且 下标从 0 开始 的数组 nextVisit 。在接下来的几天中，你访问房间的 次序 将根据下面的 规则 决定：

  • 假设某一天，你访问 i 号房间。
  • 如果算上本次访问，访问 i 号房间的次数为 奇数 ，那么 第二天 需要访问 nextVisit[i] 所指定的房间，其中 0 <= nextVisit[i] <= i 。
  • 如果算上本次访问，访问 i 号房间的次数为 偶数 ，那么 第二天 需要访问 (i + 1) mod n 号房间。

请返回你访问完所有房间的第一天的日期编号。题目数据保证总是存在这样的一天。由于答案可能很大，返回对 109 + 7 取余后的结果

暴力超时：简陋的动态规划

虽然超时了但是思路跟答案是一样的。

分析题意发现 nextVisited[i]的范围属于 [0,i]，意味着当你首次到达房间 i 时会回退到房间 nextVisited[i]。而只有访问过该房间偶数次时才会到达下一个房间，进而推断出到达 i 时，[0,i)的房间已经被访问过偶数次。

定义 f[i] 表示从奇数次到房间 i，到奇数次到达房间 i+1 所需要的天数。以下用 to 代表 nextVisited[i]，回退到房间 to 时是奇数次访问，又需要花费 f[to] 才会到达房间 to+1。从 iii 访问 to 和 i+1 又分别需要花费一天，所以有转移方程:

$$
f[i] = \sum\limits_{j=to}^{i-1}f[j]+2
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int firstDayBeenInAllRooms(int[] nextVisit) {
        int[] dp = new int[nextVisit.length];
        int MOD = 1000000007;
        for (int i = 0; i < nextVisit.length; i++) {
            //第一次进来然后去nextVisited[i]，第二次回来才变成偶数
            int temp = 2;
            //访问到nextVisited[i]，把之后所有的都会再访问一遍，全部都加起来
            for (int j = nextVisit[i]; j < i; j++) {
                temp = (dp[j]+temp)%MOD;
            }
            dp[i] = temp;
        }
        int ans = 0;
        //dp存放的只是这个节点的次数，要总体的还要全部加起来
        for (int i = 0; i < nextVisit.length-1; i++) {
            ans=(dp[i]+ans)%MOD;
        }
        return ans;
    }

}

时间复杂度o(n^2)，那肯定暴力超时

优化版：前缀和

定义前缀和
$$
s[0]=0,s[i+1] = \sum\limits_{j=0}^{i}f[i]
$$

对于
$$
f[i] = \sum\limits_{j=to}^{i-1}f[j]+2
$$
可以化简为
$$
f[i] = 2+s[i]-s[j]
$$
对于前缀和 s，有如下递推式
$$
s[i+1] = 2*s[i]-s[j]+2
$$
这样我们就不用计算原先的dp数组，通过前缀和就得到答案。

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int firstDayBeenInAllRooms(int[] nextVisit) {
        final long MOD = 1_000_000_007;
        int n = nextVisit.length;
        long[] s = new long[n];
        for (int i = 0; i < n - 1; i++) {
            int j = nextVisit[i];
            s[i + 1] = (s[i] * 2 - s[j] + 2 + MOD) % MOD; // + MOD 避免算出负数
        }
        return (int) s[n - 1];
    }
}

221 最大正方形（Medium）

在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内，找到只包含 ‘1’ 的最大正方形，并返回其面积。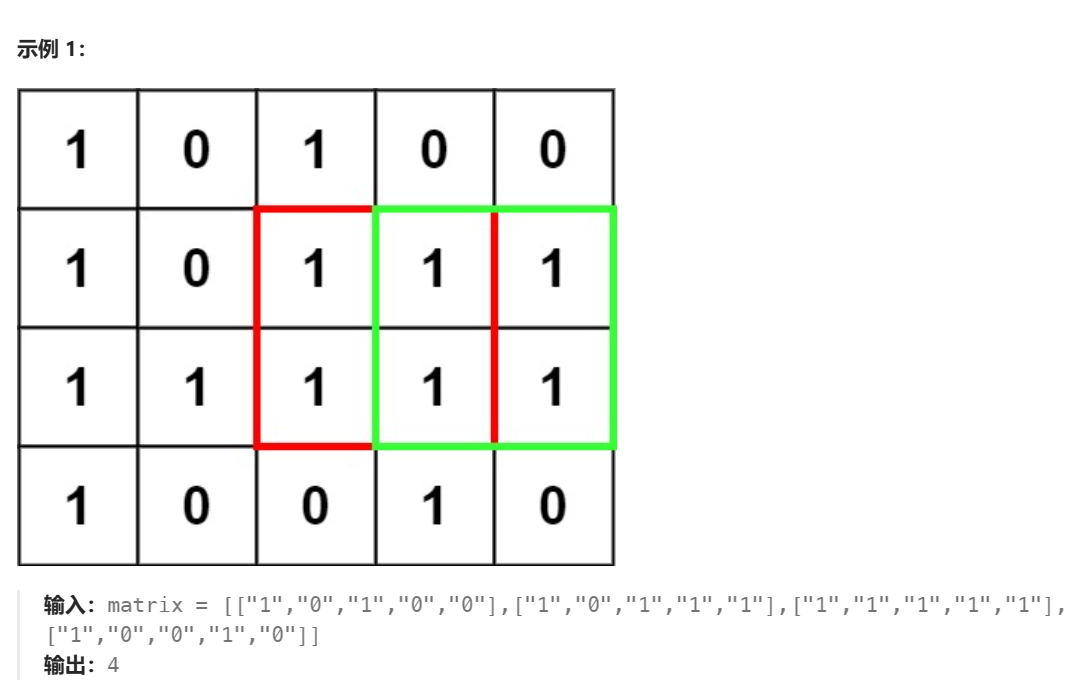

由于是在上课的时候看的，没有自己动手写，直接看的答案。我估计自己写也是智能暴力解法

二维动态规划

有点像“编辑距离”和某一天的那个截木块的每日一题，$dp[i][j]$表示以这个点为右下角的最大正方形的边长，那么如果$matrix[i][j]=0$，那dp肯定也为0，我们考虑为1的情况。

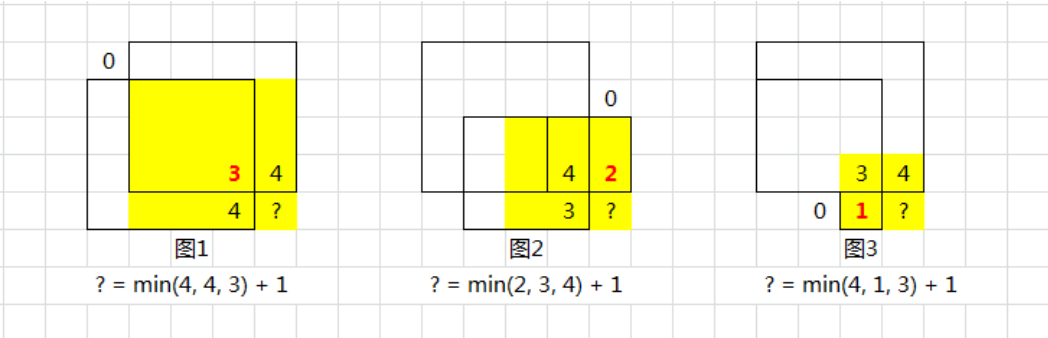
这里的状态转移方程是
$$
dp[i][j] = min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1
$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
class Solution {
    public int maximalSquare(char[][] matrix) {
        int[][] dp = new int[matrix.length][matrix[0].length];
        int ans = 0;
        for (int i = 0; i < dp.length; i++) {
            for (int j = 0; j < dp[0].length; j++) {
                if (i != 0 || j !=0){
                    if (matrix[i][j] == '1'){
                        int left = 0,up = 0,up_left = 0;
                        if (i-1 >= 0){
                            up = dp[i-1][j];
                        }
                        if (j-1 >=0){
                            left = dp[i][j-1];
                        }
                        if (i-1 >=0 && j-1>=0){
                            up_left = dp[i-1][j-1];
                        }
                        dp[i][j] = Math.min(Math.min(left,up),up_left)+1;
                        ans = Math.max(ans,dp[i][j]);
                    }
                }
                else {
                    if (matrix[i][j] == '1'){
                        dp[i][j] = 1;
                        ans = Math.max(ans,dp[i][j]);
                    }
                    else {
                        dp[i][j] = 0;
                    }
                }

            }
        }
        //System.out.println(Arrays.deepToString(dp));
        return ans*ans;
    }
}