2580 统计将重叠区间合并成组的方案数(Medium)
给你一个二维整数数组 ranges ,其中 ranges[i] = [starti, endi] 表示 starti 到 endi 之间(包括二者)的所有整数都包含在第 i 个区间中。
你需要将 ranges 分成 两个 组(可以为空),满足:
每个区间只属于一个组。
两个有 交集 的区间必须在 同一个 组内。
如果两个区间有至少 一个 公共整数,那么这两个区间是 有交集 的。
比方说,区间 [1, 3] 和 [2, 5] 有交集,因为 2 和 3 在两个区间中都被包含。
请你返回将 ranges 划分成两个组的 总方案数 。由于答案可能很大,将它对 109 + 7 取余 后返回。
示例 1:
输入:ranges = [[6,10],[5,15]]
输出:2
解释:
两个区间有交集,所以它们必须在同一个组内。
所以有两种方案:
- 将两个区间都放在第 1 个组中。
- 将两个区间都放在第 2 个组中。
区间合并+组合数
思路是将里面的区间先合并,得到长度。然后就相当于两个桶子,最终的结果为组合数相加,也就是一个杨辉三角,那么一行的总数就是2^n
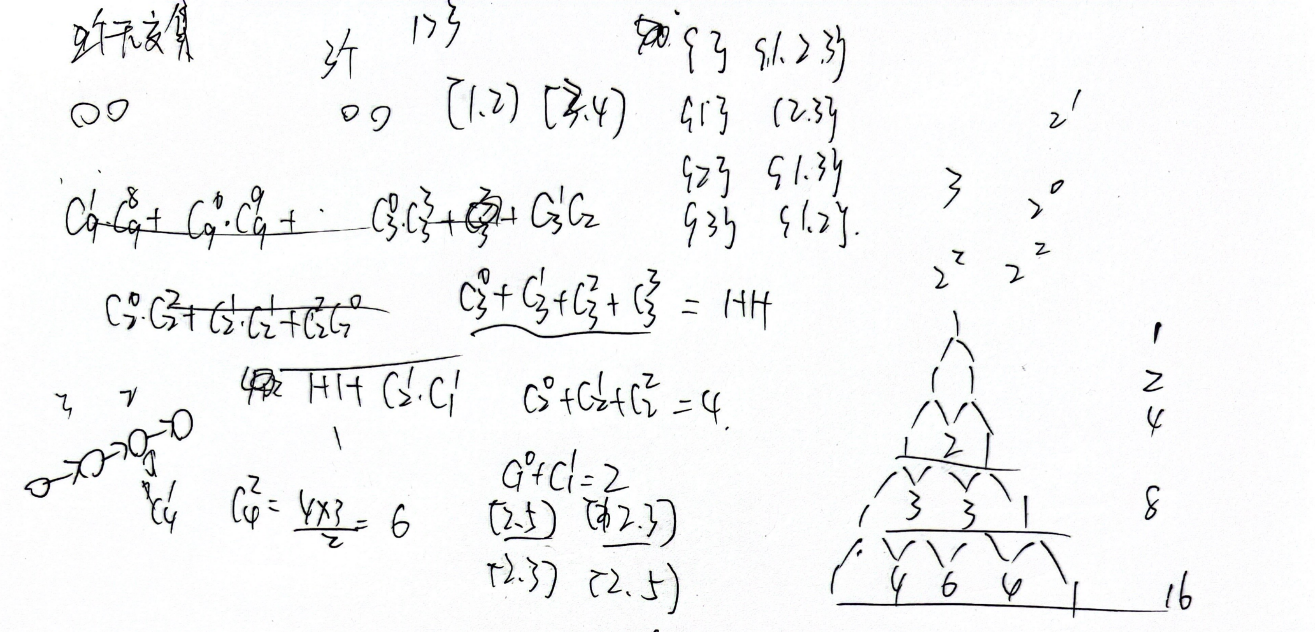
区间合并:设置一个动态数组,首先按照左括号排序,接着从后往前遍历,如果两个区间存在重合,就把后面的删除,前面的改成合并以后的新区间。
这样主要是可以避免下标的影响,从前面遍历删除会乱序号
但是这样还不够,比如这个例子[[2,3],[4,5],[6,7],[8,9],[1,10]],排序以后[[1,10],[2,3],[4,5],[6,7],[8,9]],这样以来排序也没用,结果是[[1,10],[4,5],[6,7],[8,9]],面对这种情况需要多循环几次,每次减少1个,当长度不再变化的时候就停止
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
| class Solution {
public int countWays(int[][] ranges) {
int MOD = 1000000007;
int length = merge(ranges).length;
int ans = 1;
for (int i = 0; i < length; i++) {
ans = ans *2%MOD;
}
return ans;
}
public int[][] merge(int[][] intervals){
int[][] temp1 = mergeTemp(intervals);
int[][] temp2 = mergeTemp(temp1);
while (temp1.length != temp2.length){
temp1 = mergeTemp(temp2);
temp2 = mergeTemp(temp1);
}
return temp1;
}
public int[][] mergeTemp(int[][] intervals) {
Arrays.sort(intervals, new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
if(o1[0]==o2[0]){
return o1[1] - o2[1];
}
return o1[0] - o2[0];
}
});
List<int[]> arrList = new ArrayList<>();
int rear = intervals.length-1;
for (int[] interval : intervals) {
arrList.add(interval);
}
while (rear > 0){
int[] front = arrList.get(rear-1);
int[] behind = arrList.get(rear);
int temp;
if (front[1] >= behind[0]){
temp = Math.max(front[1],behind[1]);
arrList.set(rear-1,new int[]{
arrList.get(rear-1)[0],temp
});
arrList.remove(rear);
rear--;
}
else rear--;
}
int[][] ans = new int[arrList.size()][2];
for (int i = 0; i < arrList.size(); i++) {
ans[i] = arrList.get(i);
}
return ans;
}
}
|
当初在做合并区间的时候就有点侥幸了,这个题后续还要多看
25 K个一组翻转链表(Hard)
给你链表的头节点 head ,每 k 个节点一组进行翻转,请你返回修改后的链表。
k 是一个正整数,它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换
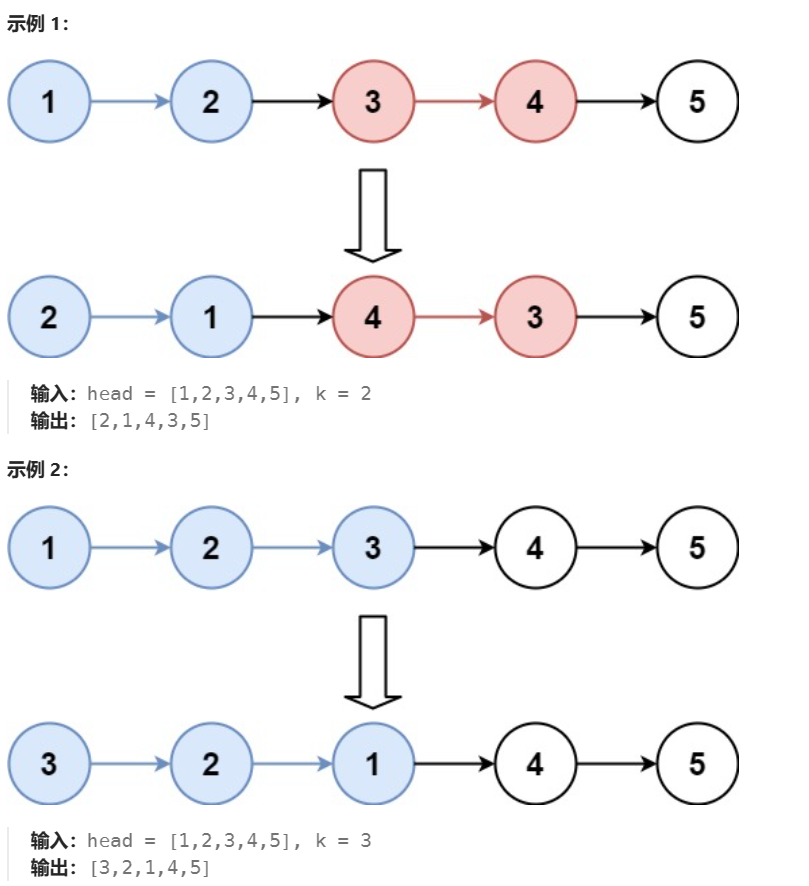
其实也没那么Hard,就是麻烦了一点
模拟
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
| class Solution {
public ListNode reverseKGroup(ListNode head, int k) {
if (k==1){
return head;
}
ListNode p = head;
int count = 0;
while (p!=null){
count++;
p = p.next;
}
p = head;
ListNode pre = head;
List<ListNode> listNodes = new ArrayList<>();
for (int i = 1; i <= count / k; i++) {
pre = getNext(pre,k);
listNodes.add(reverse(p,k));
p = pre;
}
ListNode temp = listNodes.get(0);
for (int i = 0; i < listNodes.size()-1; i++) {
temp= listNodes.get(i);
while (temp.next != null){
temp = temp.next;
}
temp.next = listNodes.get(i+1);
}
while (temp.next != null){
temp = temp.next;
}
temp.next = pre;
ListNode ans = listNodes.get(0);
return listNodes.get(0);
}
public ListNode getNext(ListNode p,int k){
for (int i = 0; i < k; i++) {
p = p.next;
}
return p;
}
public ListNode reverse(ListNode head,int k){
ListNode ans = head;
for (int i = 0; i < k - 1; i++) {
ans = ans.next;
}
ListNode pre =null,p = head,pa;
for (int i = 0; i < k; i++) {
pa = p.next;
p.next = pre;
pre = p;
p = pa;
}
return ans;
}
}
|
136 只出现一次的数字(Easy)
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
示例 1 :
输入:nums = [2,2,1]
输出:1
哈希表
这里我的思路是遍历一次然后加入哈希表进行统计,再遍历一次哈希表找出其中为1的,这样时间空间复杂度肯定都0(n)了
技巧-位运算
通过异或,因为只有两个两个的,两个相同的异或结果就是0,0和任何异或都是自身,那么所有进行异或得到的就是落单的
1
2
3
4
5
6
7
8
9
10
| class Solution {
public int singleNumber(int[] nums) {
int single = 0;
for (int num : nums) {
single ^= num;
}
return single;
}
}
|