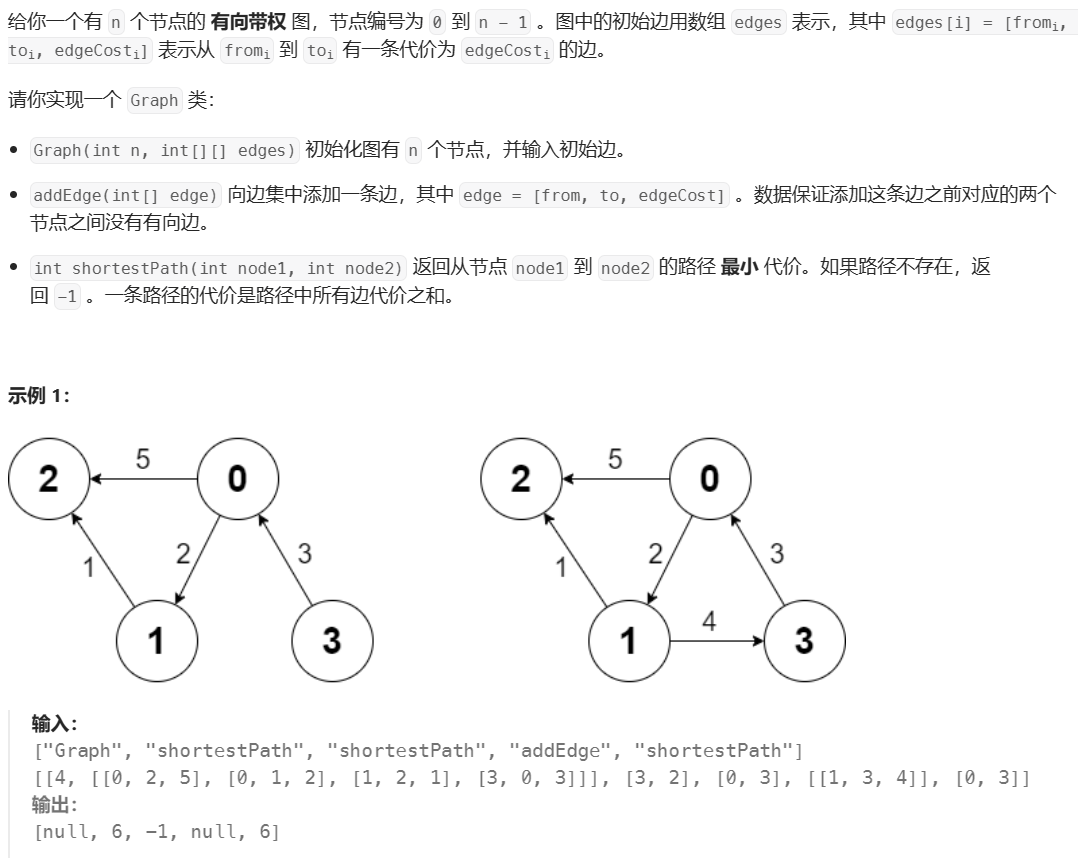
2642 设计可以求最短路径的图类（Hard）

题目太长了就换成图片了

迪杰斯特拉

我自己的做法是Dijkstra+邻接矩阵，还可以有Floyd，考虑到这个邻接矩阵都已经内存99%了，所以应该矩阵+Floyd是最佳方案

就当是复习Dijkstra了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
class Graph {

    private int[][] matrix;
    private int[] finalArr;
    private int[] visited;
    //用邻接矩阵表示图
    public Graph(int n, int[][] edges) {
        matrix = new int[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                if (i != j){
                    matrix[i][j] = Integer.MAX_VALUE;
                }
            }
        }
        for (int i = 0; i < edges.length; i++) {
            matrix[edges[i][0]][edges[i][1]] = edges[i][2];
        }
    }
    //增加一条边就是再改一个值
    public void addEdge(int[] edge) {
        matrix[edge[0]][edge[1]] = edge[2];
    }

    /**
     * Dijkstra，n次找到n个最短路径，所以需要一个visited矩阵保存已经找到最短路径的点
     * finalArr存放最短路径，初始化为初始点的邻接数组，每次找到其中最小的
     * 更新距离
     * @param node1
     * @param node2
     * @return
     */
    public int shortestPath(int node1, int node2) {
        finalArr = matrix[node1].clone();
        visited = new int[matrix.length];
        //System.out.println(Arrays.toString(finalArr));
        int k = node1;
        for (int i = 0; i < matrix.length-1; i++) {
            visited[k] = 1;
            int[] adj = getMin(finalArr);
            k = adj[0];
            int price = adj[1];
            //如果这里返回-1说明找不到最小值，最小值都已经是正无穷了
            //说明此时其他的都已经最优，直接跳出循环
            if (k ==-1){
                break;
            }
            for (int j = 0; j < matrix.length; j++) {
                if (matrix[k][j] != Integer.MAX_VALUE&&price != Integer.MAX_VALUE && visited[j] == 0 && matrix[k][j]+price < finalArr[j]){
                    finalArr[j] = matrix[k][j]+price;
                }
            }
            //System.out.println(Arrays.toString(finalArr));
        }
        if (finalArr[node2] == Integer.MAX_VALUE){
            return -1;
        }else {
            return finalArr[node2];
        }
    }
    public int[] getMin(int[] arr){
        int min = Integer.MAX_VALUE;
        int vexNum = -1;
        for (int i = 0; i < arr.length; i++) {
            if (visited[i] ==0 && arr[i] != 0){
                if (arr[i] <min){
                    min = arr[i];
                    vexNum = i;
                }
            }
        }
        return new int[]{vexNum,min};
    }
}

/**
 * Your Graph object will be instantiated and called as such:
 * Graph obj = new
 * Graph(n, edges);
 * obj.addEdge(edge);
 * int param_2 = obj.shortestPath(node1,node2);
 */

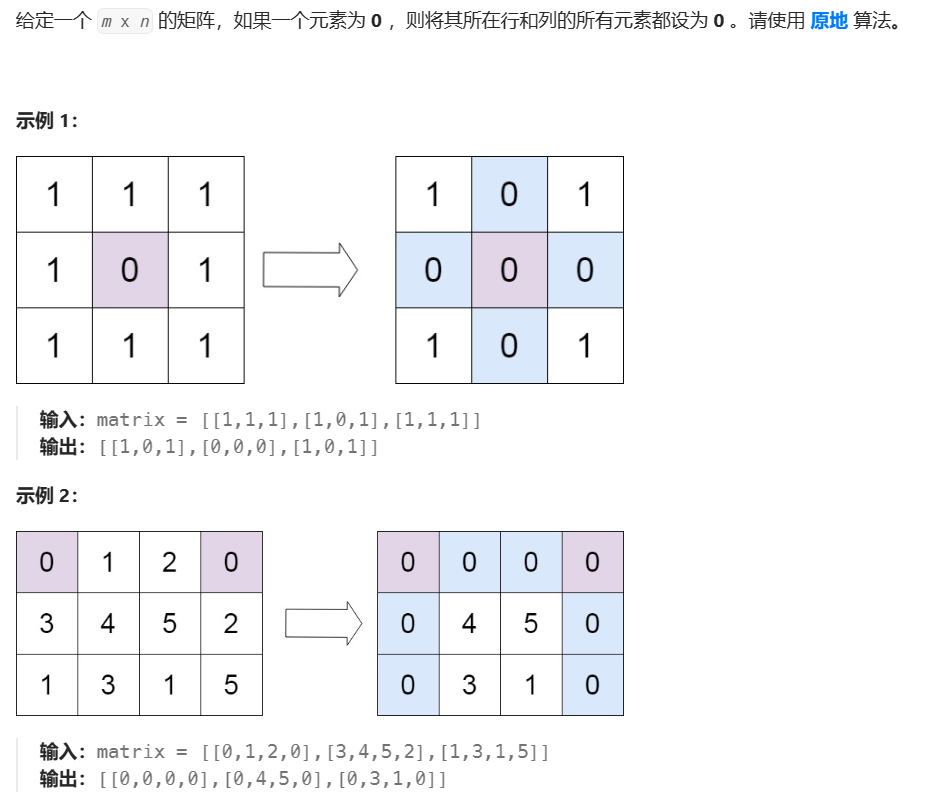
矩阵置零（Medium）

广度优先搜索

其实本来是想多源广度优先搜索的，后来发现好像不用这复杂。直接暴力每一行每一列都变成0就可以了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public void setZeroes(int[][] matrix) {
        //存储在里面找到的0
        List<int[]> points = new ArrayList<>();
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                if (matrix[i][j] == 0){
                    points.add(new int[]{i,j});
                }
            }
        }
        //遍历每一个0，使其横竖都变为0
        for(int[] point:points){
            for (int i = 0; i < matrix.length; i++) {
                matrix[i][point[1]] = 0;
            }
            for (int j = 0; j < matrix[0].length; j++) {
                matrix[point[0]][j] = 0;
            }
        }
    }
}

row为行，col为列

时间复杂度：o(row*col)

空间复杂度：o(row+col)

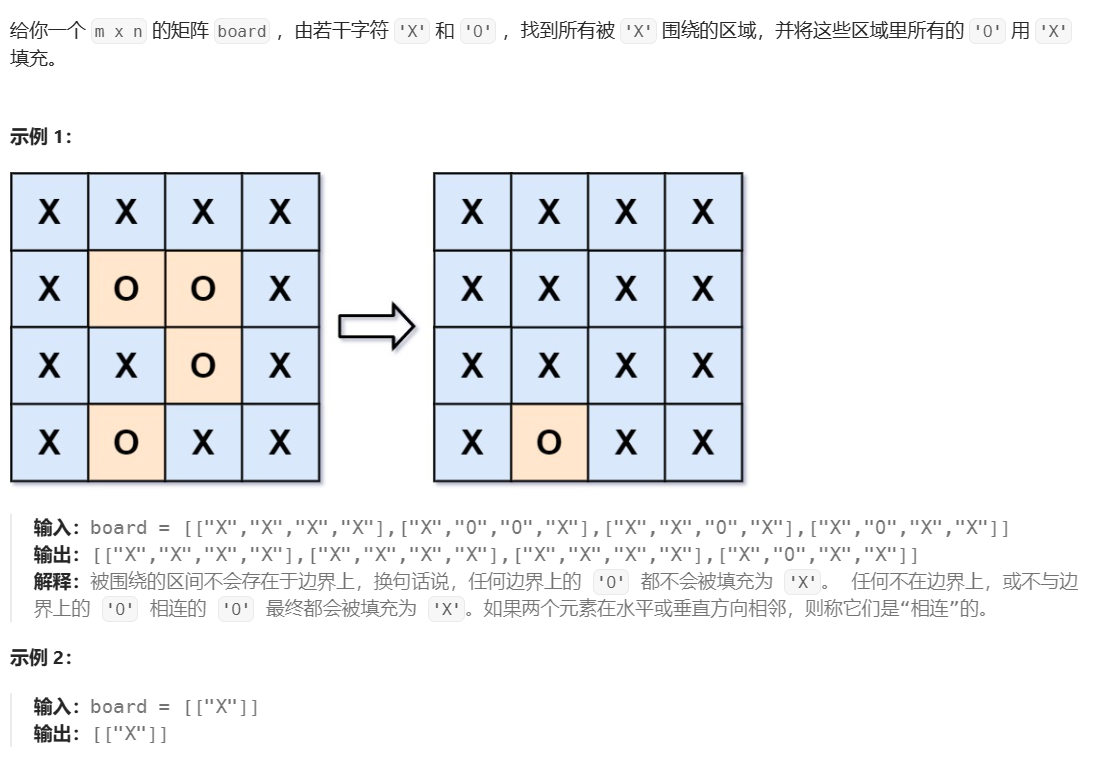
130 被围绕的区域（Medium）

深度优先搜索

主要思路是，首先找到一个区域先把其全部变为X，用一个数组保存，如果这个区域里面包含在边界的块，那么这个数组用于后续再把他变为O

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Solution {
    List<int[]> points = new ArrayList<>();
    List<List<int[]>> list = new ArrayList<>();
    public void solve(char[][] board) {
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                if (board[i][j] == 'O'){
                    points = new ArrayList<>();
                    //如果有链接到边界,随后把这些改回来
                    if (!dfs(board,i,j)){
                        list.add(points);
                    }
                }
            }
        }
        for (List<int[]> points:list){
            for (int[] point:points){
                board[point[0]][point[1]] = 'O';
            }
        }
        //System.out.println(Arrays.deepToString(board));
    }
    //一个区域块，首先全部变为X，返回真在后续把他变回O
    public boolean dfs(char[][] board,int i,int j){
        if (board[i][j] == 'O'){
            boolean temp = true;
            points.add(new int[]{i,j});
            board[i][j] = 'X';
            if (i == 0||j==0||i==board.length-1||j==board[0].length-1){
                temp = false;
            }
            if (i+1<=board.length-1){
                temp &= dfs(board,i+1,j);
            }
            if (i-1 >=0){
                temp &= dfs(board,i-1,j);
            }
            if (j+1 <= board[0].length-1){
                temp &= dfs(board,i,j+1);
            }
            if (j-1 >= 0){
                temp &= dfs(board,i,j-1);
            }
            return temp;
        }
        else {
            return true;
        }
    }
}

时间复杂度：o(mn)
空间复杂度：o(mn)

还有两题太简单了我就当复习了

排序链表

快速排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public int[] sortArray(int[] nums) {
        quickSort(nums,0,nums.length-1);
    
        return nums;
    }
    public void quickSort(int[] nums,int head,int rear){
        if (head < rear){
            int mid = partition(nums,head,rear);
            quickSort(nums,head,mid-1);
            quickSort(nums,mid+1,rear);
        }
    }
    public int partition(int[] arr,int head,int rear){
        int temp = arr[head];
        while(head < rear){
            //主要是要记得这里是每个都要带=，
            while (head < rear && arr[rear] >= temp){
                rear--;
            }
            arr[head] = arr[rear];
            while (head < rear && arr[head] <= temp){
                head++;
            }
            arr[rear] = arr[head];
        }
        arr[head] = temp;
        //System.out.println(Arrays.toString(arr));
        return head;
    }
}