518 零钱兑换2(Medium)
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
示例 1:
输入:amount = 5, coins = [1, 2, 5]
输出:4
解释:有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
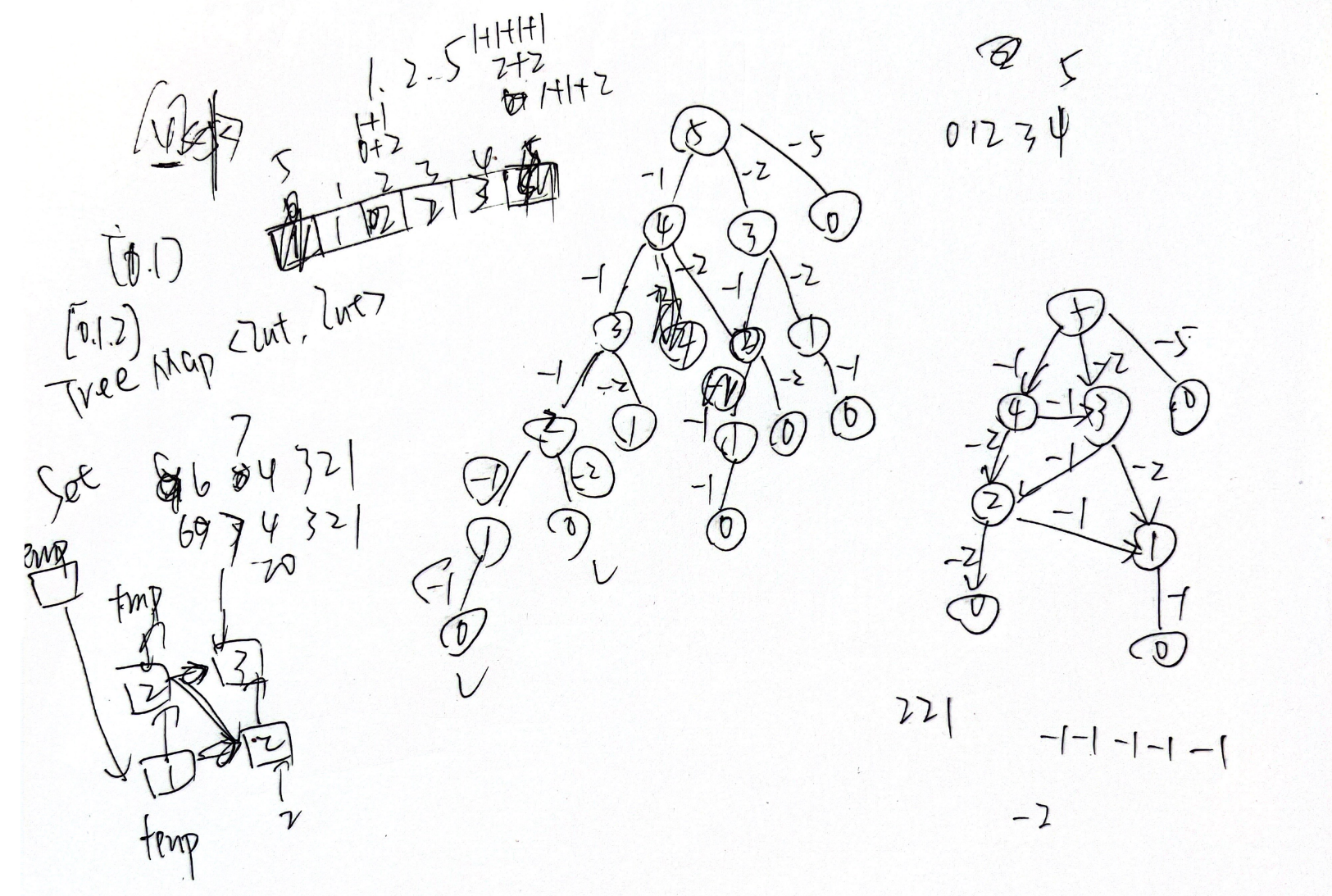
很愚蠢的暴力解:DFS(8/28)
最搞笑的是我点了一个运行,然后吃完饭都没有算出结果来,我愿称之为最暴力的一集
本意是深度优先搜索,然后将路径上的值保存进哈希表,哈希表记录的是硬币和个数,如果最后能全部找完,就把当前哈希表存到set里面(其实让我意想不到的是这样子set也可以去重)
这种方法要重复计算太多次了,可以优化成右边的有向无环图,但是就这个题而言完全没必要这么复杂。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
private HashMap<Integer,Integer> hashMap = new HashMap<>();
private Set<HashMap<Integer,Integer>> set = new HashSet<>();
public int change1(int amount, int[] coins) {
Arrays.sort(coins);
dfs(amount,coins);
return set.size();
}
public void dfs(int amount,int[] coins){
if (amount == 0){
set.add(new HashMap<>(hashMap));
return;
}
if (amount < coins[0]){
return;
}
for (int i = 0; i < coins.length; i++) {
if (!hashMap.containsKey(coins[i])){
hashMap.put(coins[i],1);
}
else {
Integer integer = hashMap.get(coins[i]);
hashMap.replace(coins[i],integer+1);
}
dfs(amount-coins[i],coins);
int temp = hashMap.get(coins[i]);
if (temp == 1){
hashMap.remove(coins[i]);
}
else {
hashMap.put(coins[i],temp-1);
}
}
}
|
动态规划(其实就是跳房子游戏)
问题一:我对这道题的主要纠结点在于,比如11,硬币有1,2,5,理应找dp[10],dp[9],dp[6],但是我们不知道这里面是不是可能造成重复,事实上dp[9]里面肯定也会只使用一个5,对于dp[6]的情况来说只是改了顺序
如何解决?我们不再遍历11而遍历硬币,这样就能保证在遍历到当前硬币之前不会有这个路径出现。每一次遍历都是如何通过当前的这个硬币换到现在的钱,
自然而然得到转移方程,dp[j] += dp[j-coins[i]];
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public int change(int amount, int[] coins) {
int[] dp = new int[amount+1];
dp[0] = 1;
for (int i = 0; i < coins.length; i++) {
for (int j = coins[i]; j < dp.length; j++) {
dp[j] += dp[j-coins[i]];
}
}
return dp[dp.length-1];
}
}
|
看完后其实是有恍然大雾的感觉,多看多学。
合并K个有序链表(Hard)
给你一个链表数组,每个链表都已经按升序排列。
请你将所有链表合并到一个升序链表中,返回合并后的链表。
实在不明白这个题怎么会是hard,给我刷战绩的题
其实还不够快,如果用分治法可以logn
队列
两两合并然后入队,直到队里面只有一个,就是答案
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| class Solution {
public ListNode mergeKLists(ListNode[] lists) {
if (lists.length == 0){
return null;
}
Queue<ListNode> queue = new ArrayDeque<>();
for (int i = 0; i < lists.length; i++) {
if (lists[i] != null){
queue.add(lists[i]);
}
}
if (queue.isEmpty()){
return null;
}
while (queue.size() != 1){
ListNode listNode1 = queue.poll();
ListNode listNode2 = queue.poll();
if (listNode1 != null && listNode2 != null){
queue.add(merge(listNode1,listNode2));
}
}
return queue.poll();
}
public ListNode merge(ListNode listNode1,ListNode listNode2){
ListNode temp = new ListNode();
ListNode ans = temp;
while (listNode1!=null && listNode2!=null){
if (listNode1.val <= listNode2.val){
temp.next = listNode1;
listNode1 = listNode1.next;
}
else {
temp.next = listNode2;
listNode2 = listNode2.next;
}
temp = temp.next;
}
if (listNode1 != null){
temp.next = listNode1;
}
if (listNode2 != null){
temp.next = listNode2;
}
return ans.next;
}
}
|
搜索二维矩阵2(Medium)
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
每行的元素从左到右升序排列。
每列的元素从上到下升序排列。
二维双指针
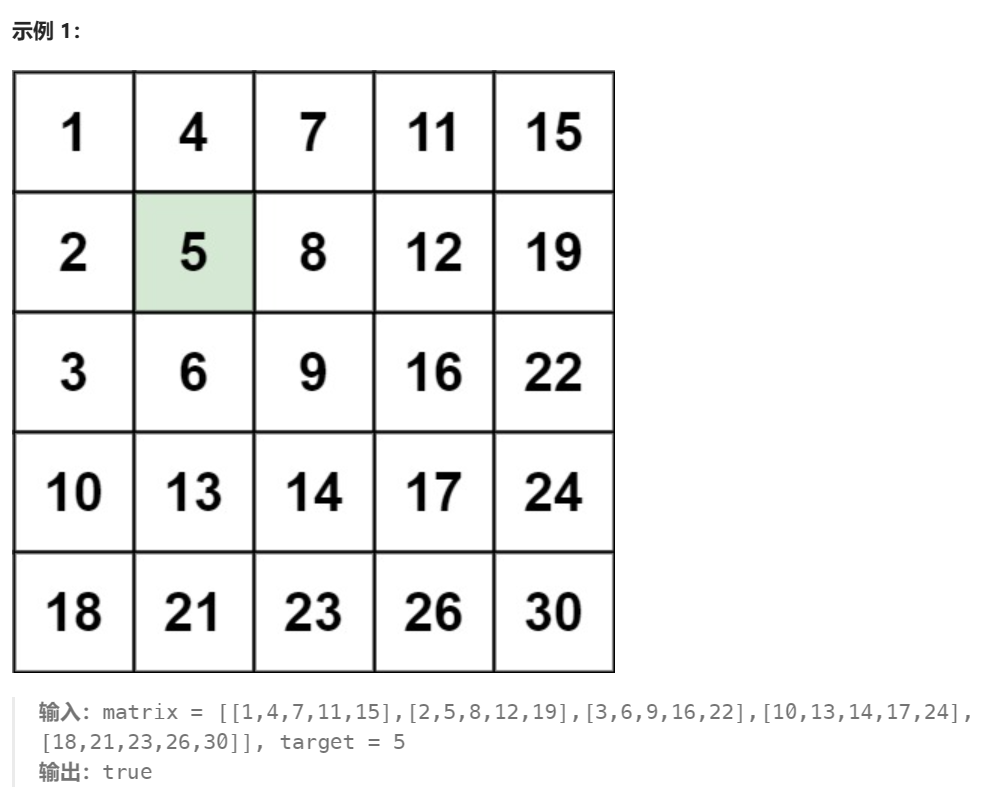
我们可以观察到,从下往上数每一行第一个元素,如果比目标大就可以删除了,同理每一列从后往前数第一个元素,如果大也可以删除了。
这样就得到了一个新矩阵。
接着找新矩阵最后一行的元素,从前往后数如果比目标小也可以删除了,然后最后一列,从上到下比目标小的也可以删除。
这样完成一次循环,减少了很大的搜索范围。一直收敛到只有一行或者一列。
这里用了小技巧,对于找不到的元素肯定是会数组下标抛异常的,catch到了肯定是没有的,返回假
还有有一个小问题,当我们面对[[5,6,9],[9,10,11],[11,14,18]]这样的数组,有两个9,这时候我们就永远满足不了循环条件出不来了,为了解决需要看循环里面四个指针是否变化,如果没变就说明发生了这种情况。直接跳出循环。而出现这种情况的原因就是因为有两个一样的目标值,那肯定返回真。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
int row_top = 0,row_bottom = matrix.length-1,col_left = 0,col_right = matrix[0].length-1;
boolean flag = false;
try {
while (row_top < row_bottom && col_left < col_right){
int temp = 0;
while (matrix[row_bottom][col_left] > target){
temp++;
row_bottom--;
}
while (matrix[row_top][col_right] > target){
temp++;
col_right--;
}
while (matrix[row_bottom][col_left] < target){
temp++;
col_left++;
}
while (matrix[row_top][col_right] <target){
temp++;
row_top++;
}
if (temp == 0){
flag = true;
break;
}
}
if (row_top == row_bottom){
for (int i = col_left; i <=col_right; i++) {
if (matrix[row_bottom][i] == target){
flag = true;
break;
}
}
}
if (col_left == col_right){
for (int i = row_top; i <= row_bottom; i++) {
if (matrix[i][col_right] == target){
flag = true;
break;
}
}
}
return flag;
}
catch (ArrayIndexOutOfBoundsException e){
return false;
}
}
}
|
这道题做出来其实有点侥幸,很多情况都是错了以后试验出来的。据他们所说这样还不如遍历整体找结果。
54 螺旋矩阵(Medium)
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
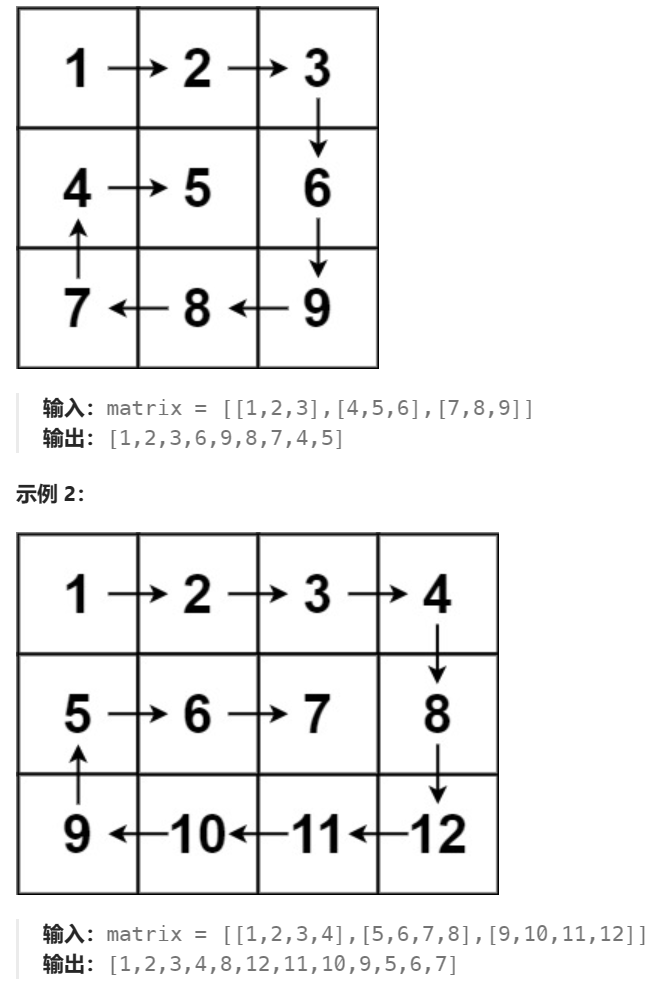
非常好理解的一道题,根据上一题的思路很快就能写出,但是这里不用频繁维护四个指针,只用在循环末尾使用就可以。
就跟洋葱一样,每次都剥掉最外一层
双指针
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
List<Integer> ans = new ArrayList<>();
int row_top = 0,row_bottom = matrix.length-1,col_left = 0,col_right = matrix[0].length-1;
while (row_top < row_bottom && col_left < col_right){
for (int i = col_left; i < col_right; i++) {
ans.add(matrix[row_top][i]);
}
for (int i = row_top; i < row_bottom; i++) {
ans.add(matrix[i][col_right]);
}
for (int i = col_right; i > col_left ; i--) {
ans.add(matrix[row_bottom][i]);
}
for (int i = row_bottom; i > row_top; i--) {
ans.add(matrix[i][col_left]);
}
row_top++;
row_bottom--;
col_left++;
col_right--;
}
if (row_top == row_bottom && col_left == col_right){
ans.add(matrix[row_top][col_right]);
}
else {
if (row_top == row_bottom){
for (int i = col_left; i <= col_right; i++) {
ans.add(matrix[row_top][i]);
}
}
if (col_left == col_right){
for (int i = row_top; i <= row_bottom; i++) {
ans.add(matrix[i][col_left]);
}
}
}
return ans;
}
}
|
59 螺旋矩阵2(Medium)
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
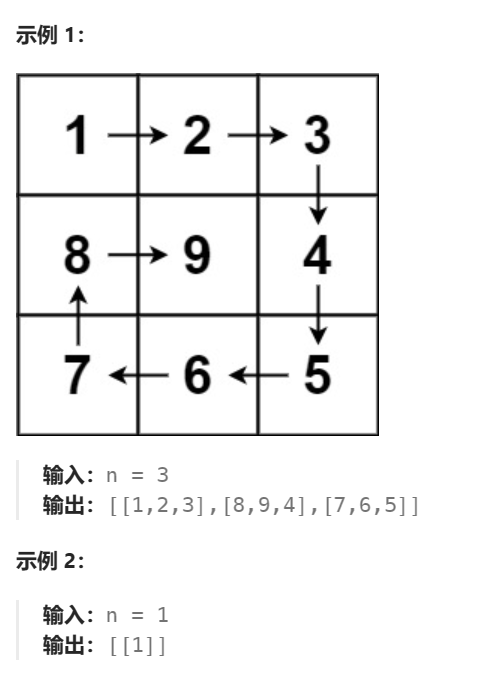
这个比上面的更简单了,一个计数器,然后根据上面的逻辑转圈,每次都+1,就可以了,甚至没有中间是一行或者一列的情况,要不就是没有要不就只有一个。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| class Solution {
public int[][] generateMatrix(int n) {
int[][] matrix = new int[n][n];
int count = 1;
int row_top = 0,row_bottom = matrix.length-1,col_left = 0,col_right = matrix[0].length-1;
while (row_top < row_bottom && col_left < col_right){
for (int i = col_left; i < col_right; i++) {
matrix[row_top][i] = count++;
}
for (int i = row_top; i < row_bottom; i++) {
matrix[i][col_right]= count++;
}
for (int i = col_right; i > col_left ; i--) {
matrix[row_bottom][i]= count++;
}
for (int i = row_bottom; i > row_top; i--) {
matrix[i][col_left]= count++;
}
row_top++;
row_bottom--;
col_left++;
col_right--;
}
if (row_top == row_bottom && col_left == col_right){
matrix[row_top][col_right]= count++;
}
else {
if (row_top == row_bottom){
for (int i = col_left; i <= col_right; i++) {
matrix[row_top][i]= count++;
}
}
if (col_left == col_right){
for (int i = row_top; i <= row_bottom; i++) {
matrix[i][col_left]= count++;
}
}
}
return matrix;
}
}
|



