323 零钱兑换(Medium)
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的。
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
今天的每日一题在十天前做过,过一遍就不重新做了
动态规划
dp数组存当前下标的钱可以用的最少兑换次数,如果用现在的零钱兑现不了,就为-1
dp[k] = min{dp[i]+dp[k-1-i]} 当且仅当dp[i]和dp[k-1-i]都不为-1
但是如果这个本身就可以用零钱找开,就为1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| class Solution {
public int coinChange(int[] coins, int amount) {
if (amount == 0){
return 0;
}
int[] dp = new int[amount+1];
for (int i = 0; i < coins.length; i++) {
if (coins[i] <= amount){
dp[coins[i]] = 1;
}
}
for (int i = 1; i <= amount; i++) {
if (i != 1){
int head = 1;
int rear = i-1;
int min = Integer.MAX_VALUE;
while (head <= rear){
if (dp[head] != -1 && dp[rear]!=-1 && dp[head] + dp[rear] < min){
min = dp[head]+dp[rear];
}
head++;
rear--;
}
if (dp[i] == 0 && min == Integer.MAX_VALUE){
dp[i] = -1;
}
if (dp[i] == 0 && min != Integer.MAX_VALUE){
dp[i] = min;
}
}
else {
if (dp[i] == 0){
dp[i] = -1;
}
}
}
return dp[amount];
}
}
|
238 除自身以外数组的乘积(Medium)
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法,且在 O(n) 时间复杂度内完成此题。
偷懒方法(就是用了除法)
最简单方法,所有乘积起来,当前元素只要除掉这个就可以,遍历一次就可以。0的时候要特殊判断一下,这个时候还是傻方法,遍历其他的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| class Solution {
public int[] productExceptSelf(int[] nums) {
int[] ans = new int[nums.length];
if (nums.length == 1){
return nums;
}
else if (nums.length > 1){
int sum = nums[0];
for (int i = 1; i < nums.length; i++) {
sum *=nums[i];
}
for (int i = 0; i < nums.length; i++) {
if (nums[i] != 0){
ans[i] = sum /nums[i];
}
else {
int front = i-1;
int next = i+1;
int anss = 1;
while (front >=0){
anss*=nums[front];
front--;
}
while (next <=nums.length-1){
anss*=nums[next];
next++;
}
ans[i] = anss;
}
}
}
return ans;
}
}
|
官方解:左右乘积列表
维护两个数组,L[i]是当前元素i左边的乘积,R[i]是i右边的乘积,返回的数组就是L[i]*R[i],每次都是o(n)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public int[] productExceptSelf(int[] nums) {
int[] L = new int[nums.length];
int[] R = new int[nums.length];
int[] ans = new int[nums.length];
L[0] = 1;
R[nums.length-1] = 1;
for (int i = 1; i < nums.length; i++) {
L[i] = L[i-1]*nums[i-1];
}
for (int j = nums.length-2; j >=0 ; j--) {
R[j] = R[j+1]*nums[j+1];
}
for (int i = 0; i < nums.length; i++) {
ans[i] = L[i] * R[i];
}
return ans;
}
}
|
11 盛最多水的容器(Medium)
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
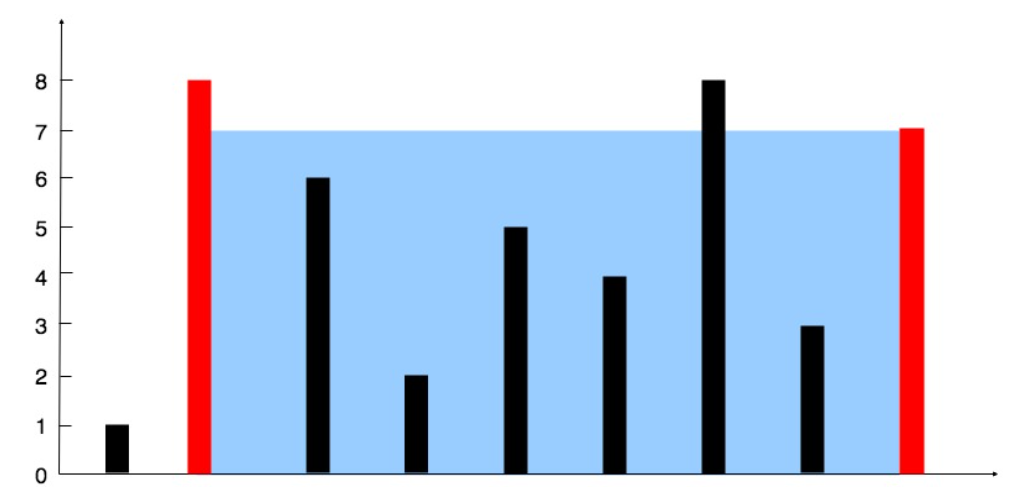
暴力超时
遍历找最小
1
2
3
4
5
6
7
8
9
10
11
| class Solution {
public int maxArea(int[] height) {
int max = Integer.MIN_VALUE;
for (int i = 0; i < height.length-1; i++) {
for (int j = i+1; j < height.length; j++) {
max = Math.max(max,(j-i)*Math.min(height[j],height[i]));
}
}
return max;
}
}
|
官方解:双指针
感觉证明有待考察,初始左右指针一个在左边一个在右边,每次移动比较小的就可以找到。


简单理解为什么移动小的,因为本来就是取较小的,移动大的话铁定没之前大,因为距离缩短了1,移动小的还可能碰到大的使原来的变大。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public int maxArea(int[] height) {
int head = 0;
int rear = height.length-1;
int max = Integer.MIN_VALUE;
while (head < rear){
int length = rear-head;
max = Math.max(max,length*Math.min(height[head],height[rear]));
if (height[head]<height[rear]){
head++;
}
else if (height[head]>height[rear]){
rear--;
}
else {
head++;
}
}
return max;
}
}
|


