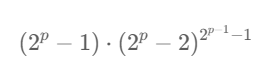1969.数组元素的最小非零乘积（Medium）

给你一个正整数 p 。你有一个下标从 1 开始的数组 nums ，这个数组包含范围 [1, 2p - 1] 内所有整数的二进制形式（两端都包含）。你可以进行以下操作任意次：

从 nums 中选择两个元素 x 和 y 。
选择 x 中的一位与 y 对应位置的位交换。对应位置指的是两个整数相同位置的二进制位。
比方说，如果 x = 1101 且 y = 0011 ，交换右边数起第 2 位后，我们得到 x = 1111 和 y = 0001 。

请你算出进行以上操作 任意次 以后，nums 能得到的 最小非零 乘积。将乘积对 109 + 7 取余后返回。

注意：答案应为取余之前的最小值。

~~自己没想出来~~，其实有思路了就是总感觉不对劲，看了答案如果继续想应该能想出来，但是问题是这个取余肯定也会困扰我很久，还有我肯定只会暴力求幂，这里的快速幂其实是很值得学习一下的

官方解：贪心+快速幂

x * y肯定是要比(x-1) * (y+1)大的，那么什么时候会有最小值呢，就是当x=1，y变得最大的时候，对于都是二进制来说，能通过交换位来变大只能是x=1,y=2^(p-1)-2了，比如3位的时候，最小就是1，最大就是6，要保持x和y互为反码

那这道题就是一个纯数学问题了，每次取两个互为反码的数都能将其变成x=1，y=2^p-2，那么一共有多少对这样的反码对呢。
n=(2^p-2)/2，除了最后面那个数其他都可以凑对，就有2^(p-1)-1对。
p=3的时候，就有3对，p=4时，就有7对

也就是说，我们的最终答案是最后一个元素*（最后一个元素-1）^(2^(p-1)-1)
即：

快速幂：通过观察 p=3的时候，就有3对，p=4时，就有7对，可以发现3就是11，7就是111，根据幂的公式x^(111)=x^(100)*x^(010)*x^(001),
答案里巧妙地用快速幂解决，也就是说，不再是暴力连乘，而是x也自己进行幂运算，就可以将复杂度降为o(log)

private static final int MOD = 1_000_000_007;
//这里的p就是已经log后的，一共有几位，每一位都循环一次
private long pow(long x, int p) {
    x %= MOD;
    long res = 1;
    while (p-- > 0) {
        res = res * x % MOD;
        x = x * x % MOD;
    }
    return res;
}

public int minNonZeroProduct(int p) {
    //移位，1L是long单位下的1，将其像左边移动p位
    //得到的k就是最后一个元素
    long k = (1L << p) - 1;
    //最后一个元素*（最后一个元素-1）^(2^(p-1)-1)
    return (int) (k % MOD * pow(k - 1, p - 1) % MOD);
}

没想出来这种方法，贪心还是练习少了

49.字母异位词分组（Medium）

给你一个字符串数组，请你将字母异位词组合在一起。可以按任意顺序返回结果列表。

字母异位词是由重新排列源单词的所有字母得到的一个新单词。

示例 1:

输入: strs = [“eat”, “tea”, “tan”, “ate”, “nat”, “bat”]
输出: [[“bat”],[“nat”,”tan”],[“ate”,”eat”,”tea”]]

自己解（也是官方解）：哈希表+排序

遍历每个字符串，然后在对其排序，如果哈希表没有就加进去，list把这个排序之前的字符串放进去，有就在哈希表已有的键里面添加这个字符串。

public List<List<String>> groupAnagrams(String[] strs) {
    HashMap<String,List<String>> hashMap = new HashMap<>();
    List<List<String>> ans = new ArrayList<>();
    for (String s:strs){
        String temp = getAllStr(s);
        //如果表里没有就新增键值对
        if (!hashMap.containsKey(temp)){
            List<String> list = new ArrayList<>();
            list.add(s);
            hashMap.put(temp,list);
        }
        //有就在末尾添加
        else {
            List<String> list = hashMap.get(temp);
            list.add(s);
            hashMap.replace(temp,list);
        }
    }
    //遍历map存在list中
    for (Map.Entry<String,List<String>> entry : hashMap.entrySet()){
        ans.add(entry.getValue());
    }
    return ans;
}
//字符串变成char数组，排序，这样就能得到唯一
public String getAllStr(String s){
    char[] temp = s.toCharArray();
    Arrays.sort(temp);
    return Arrays.toString(temp);
}

比较简单

128.最长连续序列（Medium）

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

请你设计并实现时间复杂度为 (n) 的算法解决此问题。

示例 1：

输入：nums = [100,4,200,1,3,2]

输出：4

解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

暴力解：（其实是超时的，因为复杂度为o(nlogn)）

最傻逼的一集，这里Arrays.sort就已经超出复杂度了，但是居然也没超时，甚至比超过90%，感觉有点。

最简单的思路，排序然后指针，从小到大如果一直递增就计数器一直加，如果相等那就计数器不动，如果不是，那就计数器重新变为1

public int longestConsecutive(int[] nums) {
    if (nums == null){
        return 0;
    }
    //搞笑的排序
    Arrays.sort(nums);
    int count = 1;
    int max = 1;
    for (int i = 1; i < nums.length; i++) {
        //当且仅当当前元素是之前元素的多1
        if (nums[i]==nums[i-1]+1){
            count++;
        }
        //如果相等计数器空过
        else if (nums[i] == nums[i-1]) {

        }
        //如果不是这样的情况就不是连续，计数器变成1
        else {
            count = 1;
        }
        max = Math.max(max,count);
        System.out.println(count);
    }

    return max;
}

官方解：哈希表

我们考虑枚举数组中的每个数 x，考虑以其为起点，不断尝试匹配 x+1,x+2… 是否存在，假设最长匹配到了 x+y，那么以 x 为起点的最长连续序列即为 x,x+1,x+2,x+y，其长度为 y+1，我们不断枚举并更新答案即可。

对于匹配的过程，暴力的方法是 O(n) 遍历数组去看是否存在这个数，但其实更高效的方法是用一个哈希表存储数组中的数，这样查看一个数是否存在即能优化至 O(1) 的时间复杂度。

仅仅是这样我们的算法时间复杂度最坏情况下还是会达到 O(n2)
即外层需要枚举 O(n) 个数，内层需要暴力匹配 O(n) 次），无法满足题目的要求。但仔细分析这个过程，我们会发现其中执行了很多不必要的枚举，如果已知有一个 x,x+1,x+2,⋯,x+y 的连续序列，而我们却重新从 x+1，x+2 或者是 x+y 处开始尝试匹配，那么得到的结果肯定不会优于枚举 x 为起点的答案，因此我们在外层循环的时候碰到这种情况跳过即可。

那么怎么判断是否跳过呢？由于我们要枚举的数 x 一定是在数组中不存在前驱数 x−1 的，不然按照上面的分析我们会从 x−1 开始尝试匹配，因此我们每次在哈希表中检查是否存在 x−1 即能判断是否需要跳过了。

public int longestConsecutive(int[] nums) {
    Set<Integer> num_set = new HashSet<Integer>();
    //先去重，用集合
    for (int num : nums) {
        num_set.add(num);
    }

    int longestStreak = 0;
    //有下一个值的时候就跳掉，一定要没有下一个，这样遍历才是o(n)
    for (int num : num_set) {
        if (!num_set.contains(num - 1)) {
            int currentNum = num;
            int currentStreak = 1;
            //然后比较一下
            while (num_set.contains(currentNum + 1)) {
                currentNum += 1;
                currentStreak += 1;
            }

            longestStreak = Math.max(longestStreak, currentStreak);
        }
    }

    return longestStreak;
}

非常巧妙的o(n),这里set查询是o(1)，需要好好学习一下，多用用哈希

leetcode-2024-3-20

文章目录